Bell's Theorem with Easy Math
By David R. Schneider

www.DrChinese.com

Introduction

Author's note: This article is based on Bell's Theorem (2). I have reformulated the presentation to make it a little easier to follow if your math skills are a little rusty. I follow conventional interpretation of both QM (quantum mechanics) and Bell. In this derivation, I lean heavily on the concepts presented by Mermin (4) which greatly simplifies my explanation. I have reformulated ideas for the sake of simplicity, and to the purist this presentation will surely be lacking. For a more rigorous proof, please look to the references at the end of the article. If you are interested in more of the history of Bell's Theorem, try: DrChinese Presents Bell's Theorem

Bell's Theorem is the most famous legacy of the late great J.S. Bell. Published in 1965, Bell's Theorem is famous for drawing an important line in the sand between Quantum Mechanics and the world as we know it intuitively. It is simple and elegant, and at the same time touches upon many of the fundamental philosophical issues that relate to modern physics. If you want to understand the richer meaning of Relativity and Quantum Theory, you will also want to learn about Bell. In it simplest form, Bell's Theorem states:

No physical theory of local Hidden Variables can ever reproduce all of the predictions of Quantum Mechanics.

If you are unfamiliar with the math of Bell's Theorem, or have previously found it difficult to comprehend... then perhaps this paper can help. My objective is to provide the most simple understanding of Bell's Theorem possible. I assume that the reader does NOT have a thorough understanding of either Quantum Mechanics or the math of Bell's Theorem. Yet, I will present all of the key ideas needed to understand the proof of Bell's Theorem. It's really not hard at all! The only math you need to follow is presented in a table of permutations below. Table 1 only requires understanding of very basic statistical concepts. Enjoy!


History

In 1935, Albert Einstein collaborated with Boris Podolsky and Nathan Rosen to publish a paper which is now simply referred to by the initials of its three authors: EPR (1). In essense, they concluded that Quantum Mechanics (QM) was incomplete because there existed so called "Hidden Variables" which must explain at least some of the uncertainty inherent in QM. Hidden Variables means that there are microscopic properties of fundamental particles that we are unable to observe directly by means of testing, perhaps due to technological limitations that might not exist at some future time. I.e. maybe we simply need a bigger microscope to see the details of what is going on at the very smallest level. But since we can't observe them, they may be "hidden" now - but perhaps if we knew more about them then that might explain the otherwise mysterious behavior of particles. The Heisenberg Uncertainty Principle (HUP), a key component of Quantum Mechanics, says that these variables are not just unobservable; they simply don't exist outside of the context of an observation. This deviates from our everyday view of reality.

EPR had a simple but powerful definition of what they called an "element of reality": IF an observable property of a system could be predicted with absolute certainty (100%) without disturbing that system, THEN it must correspond with an element of reality. A simple and succinct definition, to be sure. And one with which few would argue. We will use this definition in our proof of Bell's Theorem.

EPR provided a proof that says in essence: either there are Hidden Variables, OR particle attributes (such as position, velocity, energy, polarization, etc.) are not real and defined until they are observed. This part is generally accepted, and is simply an extension of the HUP. EPR also said that since it is "unreasonable" to believe that these particle attributes require observation to become real, therefore Hidden Variables must exist. Einstein said: "I think that a particle must have a separate reality independent of the measurements. That is: an electron has spin, location and so forth even when it is not being measured. I like to think that the moon is there even if I am not looking at it." This second part of EPR was accepted by some, and rejected by others including Bell.

After all, QM actually says that an observation does shape reality - and can do so even after the fact! A strange position, to be sure, but not contradicted by the facts. Building from this position, Bell then went further: he showed that local Hidden Variables would lead to a disagreement with the predictions of QM in certain specific cases. So Bell's Theorem is based on EPR. The Hidden Variable scenarios impose a critical requirement which was not obvious. 30 years after EPR, Bell exposed this requirement, which is referred to as Bell's Inequality.


Photon Polarization

Let's consider the case of the polarization of light. A particle of light is called a photon. Most photons are linearly polarized and this polarization can be observed (measured) using a polarizer filter or a polarizer crystal. Polarizing sunglasses use this polarization characteristic as the basis for their operation. As a general rule, half of all RANDOMLY polarized light will pass through a polarizing filter. The other half will be reflected/absorbed by the filter. This is true regardless of the orientation of the filter. Generally, the filter can be set at any angle from 0 degrees to 360 degrees - i.e. it can be rotated at will in a circle. These effects are seen even if the light source is made to be so weak that a single photon passes though at a time! Once any photon passes through a polarizer lens, its polarization will be aligned exactly with the lens thereafter (even if it wasn't previously).

Suppose we consider a single particle (photon) of light. We ask a simple question: does it have a definite polarization at the following three angles: 0 degrees (A), 120 degrees (B), and 240 degrees (C)? According to the EPR paper, its polarization at these 3 angles correspond to actual elements of reality IF they can be predicted with certainty without disturbing the system. This can be confirmed via conventional optics: any photon with a known polarization (say 0 degrees) can be checked at a later time by another polarizer at the same angle setting. The predicted result (100% certainty) is that the photon will have the same polarization at that later time, and this has been known to be true for about 200 years (Malus, 1809). By extension, A, B and C must correspond individually to elements of reality, according to the definition of EPR. (In fact, any angle's polarization will meet this test individually.)

Next we come to the $64,000 question: do A, B and C correspond to SIMULTANEOUS elements of reality? You see, the test we describe above only works for one angle at a time. We can test A, B or C one at a time, but there is no way to test for all 3 simultaneously. Yet according to EPR, an element of reality exists independent of the act of observation. I.E. all elements of reality have definite values at all times, EVEN IF WE DON'T KNOW THEIR VALUES. In fact, EPR says that any other position would be unreasonable. So according to this view, angles A, B and C must have simultaneous definite answers to the questions of their polarizations - even if they cannot be known. So at angle A there might be a hidden variable A; and at angle B we have hidden variable B; and and at angle C we have hidden variable C. If only we had the tools, perhaps we could aspire to someday be able to simultaneously observe the hidden variables A, B and C of a single photon. We want to imagine here that even if the actual values of the photon's "Hidden Variables" seem capricious or random, they must be SOMETHING.

Or not! Let's see where this seemingly reasonable assumption leads us. The proof is less than a dozen paragraphs, with one table. And EASY MATH that anyone can follow!










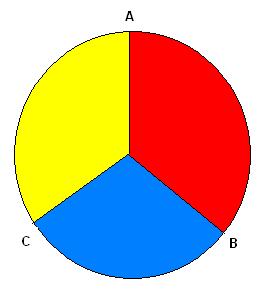
Figure 1:
We can't explain why a photon's polarization takes on the values it does at angle settings A, B and C. But we can measure it after the fact with a polarizer at one setting, and in some cases we can predict it for one setting in advance. The colors match up with the columns in Table 1 below. (By convention, the 0 degrees alignment corresponds to straight up.)



Proof

a. ASSUME that a photon has 3 simultaneously real Hidden Variables A, B and C at the angles 0 degrees, 120 degrees and 240 degrees per the diagram above. These 3 Hidden Variables, if they exist, would correspond to simultaneous elements of reality associated with the photon's measurable polarization attributes at measurement settings A, B and C. In other words, each hidden variable gives us the answer to the question "will this photon pass through a polarizer lens set at a specific angle?" Presumably, this information is SOMEHOW encoded definitely in the photon at the time it is created (sort of like an instruction set) and does NOT depend in any way on the polarizer lens itself (which is encountered at a later time).

This the FIRST and primary assumption we need for Bell's Theorem. This is also the minimum definition of any Hidden Variables theory. I call this assumption "Bell Reality". And... this assumption is the equivalent of assuming that the moon is there when no one looks. After all, we are simply saying that the answers to the 3 questions "What is the polarization of a photon at: 0, 120 and 240 degrees?" exist independently of actually seeing them. If a photon has definite simultaneous values for these 3 polarization settings, then they must correspond to the 8 cases ([1]...[8]) presented in Table 1 below. So our first assumption is that reality is independent of observation, and we will check and see if that assumption holds up.

b. Now we will ask another simple question: if we measured the polarization at any one of the 3 angles, what is the likelihood that a neighboring measurement at one of the other two angles will agree with the results of the first? For example, if we knew the polarization at A, what is the likelihood that B would be the same? Or if we knew the polarization at B, what is the likelihood that C would be the same? Or if we knew the polarization at C, what is the likelihood that A would be the same?

There are only three angle pairs to consider in the above: A and B (we'll call this [AB]); B and C (we'll call this [BC]); and lastly A and C (we'll call this [AC]). If A and B yielded the same values (either both + or both -), then [AB]=matched and we will call this a "1". If A and B yielded different values (one a + and the other a -), then [AB]=unmatched and we will call this a "0". Ditto for [BC] and [AC]. If you consider all of the permutations of what A, B and C can be, you come up with the following table:

Case	A=0 degrees	B=120 degrees	C=240 degrees	[AB]	[BC]	[AC]	Sum [AB]+[BC]+[AC]	Average ([AB]+[BC]+[AC]/3)
[1]	A+	B+	C+	1 (++)	1 (++)	1 (++)	3	1.000
[2]	A+	B+	C-	1 (++)	0	0	1	.333
[3]	A+	B-	C+	0	0	1 (++)	1	.333
[4]	A+	B-	C-	0	1 (--)	0	1	.333
[5]	A-	B+	C+	0	1 (++)	0	1	.333
[6]	A-	B+	C-	0	0	1 (--)	1	.333
[7]	A-	B-	C+	1 (--)	0	0	1	.333
[8]	A-	B-	C-	1 (--)	1 (--)	1 (--)	3	1.000

Table 1:
Permutations of A, B and C with likelihood of matches (++ or --). All we have done is listed all of the possibilities, and calculated the averages of random tests of the pairs [AB], [BC] and [AC] for each of them. That is, IF we had some way to actually test 2 settings simultaneously for one photon. Can a way be found to do this?

OK, now here is the really hard part (just kidding): it is pretty obvious from the table above that no matter which of the 8 scenarios which actually occur (and we have no control over this), the average likelihood of seeing a match for any pair must be at least .333! How could it not be? Even if you don't know which of the eight scenarios ([1]...[8]) are actually occurring, if you randomly select any of the 3 pairs ([AB], [BC] or [AC]) enough times then you would expect to get matching results (++ or --) AT LEAST a third of the time. If you are not sure of this point, then please review the table above until you are sure. Of course, keep in mind that we still have not presented any way to test 2 different settings on a single photon at the same time...yet.

Here is an example: Suppose nature deals us case [5] above. We have no control over that, and won't actually be sure we were given case [5]. In this case, if happen to select to test the [AB] or [AC] pairs (which is something that we, as observers, will do randomly and do have control over) then we will not get a match. That will happen 2/3 of the time. But the other 1/3 of the time, we would get the [BC] pair to test and we would see a match. This gives us a rate of matches of 1/3 (or .333). Most of the cases work out like [5]: [2], [3], [4], and [6] all do. Cases [1] and [8] actually always yield matches (3/3 or 100% of the time). We don't know whether these particular cases happen very often, but you can see that for any case the likelihood of a match is either 1/3 or 3/3). Thus you never get a rate less than 1/3 as long as you sample [AB], [BC] and [AC] evenly.

The fact that the matches should occur greater than or equal to 1/3 of the time is called Bell's Inequality. More specifically, the value of Bell's Inequality at 120 degrees is 1/3 (at least in this formulation - there are other formulations that accomplish the same basic result). We have deduced this requirement simply from assuming simultaneous Hidden Variables per a. above. (In fact, this minimum value actually applies to ANY 3 angles that we could choose, not just the 0/120/240 degree cases shown above. However, we chose these angles for a reason which will become clear below.)

c. Importantly, Bell also noticed that QM predicts that the actual value will be .250, which is LESS than the "Hidden Variables" predicted value of at least .333. It doesn't really matter where the QM predicted value of .250 comes from, but I'll tell you anyway: it is the square of the cosine of the angle between the 2 polarizer settings, which is 120 degrees (regardless of whether we are talking about [AB], [BC], or [AC]). The cosine of 120 degrees is -.500 (you can look that up on your computer's calculator - type in 120 and press COS); and that squared (-.500 x -.500) is .250 (or 1/4). Not too hard!

We're done! We have proved the main component of Bell's Theorem: that the predictions of any Hidden Variables theory (1/3 or greater) are incompatible with the predictions of Quantum Mechanics (1/4). Bell does not tell us whether it is Quantum Mechanics or Hidden Variables which is correct - in fact they could both be wrong. But they cannot both be right. That didn't hurt, did it?

d. Bell anticipated that this result sounded good in theory, but needed more to make sense - because the above conclusion could not be tested. And in his next step he once again drew from EPR. He was aware that it was theoretically possible to have entangled particles that had identical but unknown spin attributes. Using these entangled particles, it would be possible to measure 2 of the 3 settings mentioned above simultaneously, thus providing a way to differentiate between QM and Hidden Variables experimentally using Bell's Inequality. Measure one attribute (say A) on one particle (let's call this Alice); then measure a different attribute (say B) on the other particle (let's call it Bob). Since Alice and Bob have identical attributes, a measurement of B on Bob tell you indirectly about B on Alice. You tested A on Alice directly, and now know B about Alice indirectly, so now you know about A and B for Alice.

But there was a price to pay for such this experimental setup: we must add a SECOND assumption. That assumption is: A measurement setting for one particle does not somehow affect the outcome at the other particle if those particles are space-like separated. This is needed because if there was something that affected Alice due to a measurement on Bob, the results would be skewed and the results could no longer be relied upon as being an independent measurement of a second attribute. This second assumption is called "Bell Locality" and results in a modification to our conclusion above. In this modified version, we conclude: the predictions of any LOCAL Hidden Variables theory are incompatible with the predictions of Quantum Mechanics. Q.E.D.


After Bell

So the last step is one you can see coming: perform an EXPERIMENT that tests the above; then see if the results are closer to QM's prediction of .250 or to the Local Hidden Variables scenario (i.e. at least .333). They cannot both be right. If they are NOT in accordance with the .333 prediction, then our initial assumption above - that A, B and C exist simultaneously - must be WRONG. Please recall: a single counter-example is sufficient to disprove any theory, and this forms the basis of our conclusion.

The results: Experiments support the predictions of QM. The measured value for the matches at 120 degrees is very nearly .250 just as QM predicts. As a practical matter, the experiments are set up differently than described here; and a different version of Bell's Inequality - called the CHSH Inequality - is what is actually analyzed. See these actual experiments, which seem to defy common sense! See also Aspect's 1981 work (4), which is considered definitive. This result means that our seemingly reasonable assumption (that there are simultaneous Hidden Variables) that we started with in a. above is invalid. This is easily explained in QM because QM says that particle attributes only exist within the context of an actual measurement. Therefore, we must conclude that the moon is NOT there when we are not looking at it (so to speak). This is the end result of Bell's Theorem.

Please note that there is a way out of this seemingly impossible scenario, but the loophole may be difficult to swallow: if Einstein's Relativity is wrong, and the speed of light is NOT a limit for propagation of cause and effect (which is called "signal locality"), then that would give us a way out of the situation. Theoretically, there could exist non-local hidden variables (Bohm outlined such a theory, for example). But regardless, the net effect of Bell's Theorem is profound. Reality is somehow dependent upon how we observe it.



References

(1) A. Einstein, B. Podolsky, N. Rosen: "Can quantum-mechanical description of physical reality be considered complete?" Physical Review 41, 777 (15 May 1935).

(2) J.S. Bell: "On the Einstein Podolsky Rosen paradox" Physics 1 #3, 195 (1964).

(3) A. Aspect, Dalibard, G. Roger: "Experimental test of Bell's inequalities using time-varying analyzers" Physical Review Letters 49 #25, 1804 (20 Dec 1982).

(4) N. David Mermin: "Is the moon there when nobody looks? Reality and the quantum theory" (PDF, 267k) Physics Today (April 1985)

You can view a copy of papers 1, 2 and 3 in .PDF form at: EPR, Bell and Aspect: The Original References

Some additional links for more information about Bell's Theorem:

Abner Shimony: "Bell's Theorem" (updated as of 2005). This is a top notch presentation of Bell's Theorem, very comprehensive. It provides tremendous depth on the subject by one of the pioneers of the field. It also includes an excellent bibliography. Intended for intermediate and advanced readers.

Bell's Theorem: An Overview with Lotsa Links Intended for beginning readers.

David Schneider: "Bell's Theorem and Negative Probabilities" (2005) . This is my more formal presentation of Bell's Theorem. This has deeper math than the current article, and uses a more standard approach. Intended for intermediate readers.

(c) 2005-2023 David R. Schneider.